Техника расчётов чертежа парусного судна

Это простая арифметика! Хотя суть этой арифметики — интегрирование, т. е. суммирование величин с последующим умножением на дискрет — шпацию ∆L или расстояние между ватерлиниями ∆Т. Расчеты сводятся к вычислению площадей и объемов и нахождению их центров тяжести. Приведем пример вычисления площади шпангоута (подводной части).

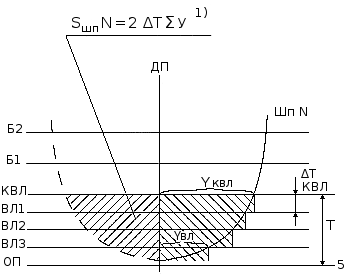
Рис. 9.7. Площадь шпангоута (подводная часть)

Численные значения величин берут из теоретического чертежа или из таблицы плазовых ординат. Важен смысл выполняемой работы — т. е. расчета площади. Таким образом, площадь подводной части шпангоута определится как сумма площадей его отдельных участков:

2 × Y_квл × ∆T + 2 × Y_вл1 × ∆Т + 2 × Y_вл2 × ∆T + 2 × Y_вл3 × ∆Т = 2 × ∆T × ∑ = Sшп№,

где: символ «∑» — означает суммирование для всех «Y».

Это несколько приближенно, однако уже достаточно. Но, если необходимо более точно, используют большее число ватерлиний в теоретическом чертеже и(или) вычитают поправки в виде 1/2(Y_квл + Y_{вл(нижн.)}). Для вычисления объемного водоизмещения используют аналогичный прием. Достаточно заполнить таблицу:

 

Шп№	1	2	3	4	5	6	7	8	9	10	11	12	13	ВЛ суммы ∑вл	Площади ВЛ = ∆L × ∑
Ординаты (Yi) на один борт
КВЛ
ВЛ1
ВЛ2
ВЛ3
Суммы ∑шп
Площади шп = ∆ × ∑шп

Водоизмещение получается суммированием всех площадей шпангоутов и умножением этой суммы на размер шпации ∆L или(и) суммированием всех площадей ватерлиний и умножением этой суммы на размер шага между ватерлиниями — ∆T. Реальное водоизмещение будет близко к среднему от вычисленных двумя путями — по шпангоутам и по ВЛ. Удобно вести все расчеты в дециметрах. Тогда объемное водоизмещение будет в дециметрах кубических — т. е. в литрах. Используя таблицу расчета водоизмещения (строка ∑шп) можно построить строевую по шпангоутам на проекции полуширота и увидеть как распределяется объем водоизмещения по длине корпуса.

Также строят кривую распределения водоизмещения по глубине трюма (строка ∑вл) на проекции корпус — это строевая по ватерлиниям. Измеряя и суммируя длины ветвей шпангоутов можно вычислить площадь поверхности корпуса, не забывая умножить полученную сумму на размер шпации ∆L. Зная площадь КВЛ в дм² не трудно сообразить как увеличится водоизмещение (V) при увеличении осадки например на 1 см (S_квл × 0,1 дм ≈ ∆V кг).